Estimación de los tiempos de desplazamiento a partir de la sinuosidad de las carreteras
Dentro de los estudios de accesibilidad y movilidad y su modelización en los Sistemas de Información Geográfica es habitual calcular los tiempos de viajes basándonos en la aplicación de algoritmos de camino más corto. En este sentido uno de las principales problemas al que nos podemos enfrentar a la hora de generar modelos de accesibilidad geográfica en un GIS en términos de distancia (tiempo y coste de recorrido) es la dificultad a la hora de calcular la velocidad real de recorrido cuando no se dispone de esta información.
La velocidad de la vía suele estar influida por factores que van desde los orográficos del propio terreno que atraviesa, a los geométricos (anchura de la plataforma, número de carriles, tipo de superficie, radios de curva mínimos, peraltes, etc.), funcionales (vías arteriales, colectoras-distribuidoras y locales) o de demanda (capacidad, Niveles de Servicio, IMD, etc.).
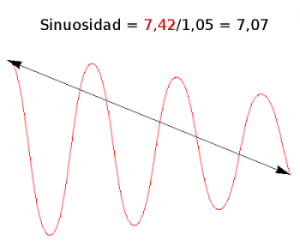
El índice de sinuosidad de un arco viene dado por el cociente de la distancia observada o real entre la distancia esperada o teórica.
No obstante, aún no teniendo este tipo de información es posibles estimar los tiempos aproximados de recorrido de cada arco de la red a través de métodos cuantificativos indirectos, como es calculando la sinuosidad y conociendo la tipología de vía.
El modelo presupone una determinada velocidad de recorrido según el grado de sinuosidad de la vía y las características determinadas de esta. Los índices de sinuosidad se han venido utilizando frecuentemente en geomorfología para clasificar las redes hidrográficas en función del serpenteo de los cauces descritos por el curso del agua (Haggett y Chorley, 1969). Para ello se utiliza una simple fórmula que divide la longitud del arco entre la longitud de la cuerda:
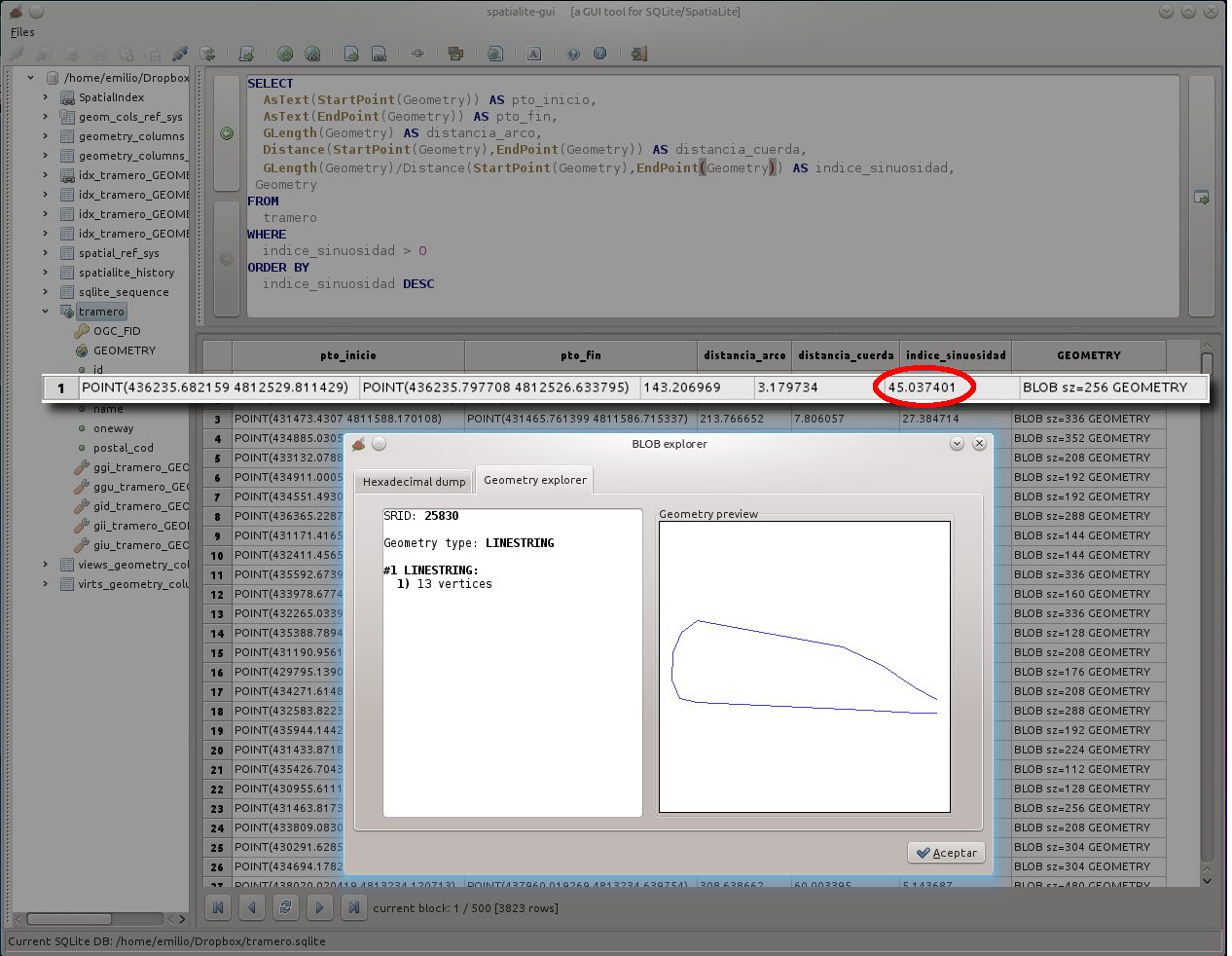
Una carretera con un índice de sinuosidad de valor 1 significa que su arco se ajusta a la recta y por lo tanto carece de curvas. Por contra la geometría del trazado se complica a medida que aumenta este índice. Veamos esto en el resultado que nos devuelve una base de datos SQLite a partir de una consulta espacial de ejemplo:
SELECT ST_AsText(ST_StartPoint(Geometry)) AS pto_inicio, ST_AsText(ST_EndPoint(Geometry)) AS pto_fin, ST_Length(Geometry) AS distancia_arco, ST_Distance(ST_StartPoint(Geometry), ST_EndPoint(Geometry)) AS distancia_cuerda, ST_Length(Geometry)/ST_Distance(ST_StartPoint(Geometry), ST_EndPoint(Geometry)) AS indice_sinuosidad, Geometry FROM tramero WHERE indice_sinuosidad > 0 ORDER BY indice_sinuosidad DESC
En el predicado de esta sentencia SQL descartamos los arcos con un índice de sinuosidad igual a 0 ya que corresponden fundamentalmente a vías que comienzan y finalizan en el mismo punto (rotondas y cul-de-sac con retornos, principalmente). En la siguiente captura de pantalla vemos un ejemplo de un caso intenso de sinuosidad, en el que la línea tiene un índice de 45.04 debido a que su longitud real es muy grande pese a la proximidad de los extremos.
Un vez calculado el índice definiremos un umbral para clasificar una carretera como sinuosa o no. La experiencia te indica que este umbral es variable en función del conjunto del territorio que estemos analizando y atendiendo a su realidad física: no es lo mismo la modelización de la red en un territorio como Cantabria, con un tercio de este con pendientes de más del 30%, que en Valladolid, una de las provincias de España con menor desnivel medio.
El siguiente paso es calcular las velocidades medias teóricas genéricas de viaje en cada arco de la red en función de la clasificación previa. Por ejemplo, el modelo de Brabyn y Skelly (2001) asigna las siguientes velocidades estimadas:
- Vía urbana: 30 km/h
- Autopista urbana: 80 km/h
- Carretera rectilínea no urbana de dos carriles por sentidoo: 80 km/h
- Carretera sinuosa no urbana de dos carriles por sentido: 60 km/h
- Carretera rectilínea no urbana de un carril por sentido: 70 km/h
- Carretera sinuosa no urbana de un carril por sentido: 40 km/h
- Carretera rectilínea adoquinada, empedrada o de áridos: 50 km/h
- Carretera sinuosa adoquinada, empedrada o de áridos: 50 km/h
Esto permite extraer una matriz de velocidades y distancias con la que finalmente poder calcular los tiempos de acceso entre puntos.
Aunque este es un buen modelo de aproximación, hay que tener en cuenta que contiene errores si los arcos son excesivamente grandes, dado que líneas con similar longitud pueden tener una sinuosidad diferente que no quede reflejada en su índice. Esto quiere decir que una curva muy amplia puede ser igual a muchas curvas pequeñas a lo largo de una carretera, dando valores similares de sinuosidad para ambas vías. Para contrarrestar este efecto deberemos acortar los arcos de la red en tramos más pequeños.
Lógicamente podemos complicar el modelo tanto como queramos o podamos, añadiendo otros factores que determinan la velocidad de desplazamiento y que podemos calcular a partir de la geometría de la red u otras capas: el cálculo de la pendiente media, el radio de las curvas, la visibilidad según el desnivel y curvatura de la carretera, tipo de condición de suelo por el que atraviesa (rural o urbano), etc. Finalmente puede ser necesario reajustar los cálculos en función de nuestra experiencia o a través de trabajo en campo, a partir de la toma de medidas en determinados arcos de la red mediante vehículo flotante.

GIS Project Manager en Alter Geosistemas. Es geógrafo con amplia experiencia profesional en el ámbito de la geomática y las tecnologías afines. Ha dirigido y participado en numerosos proyectos de consultoría e ingeniería en las fases de planificación, ejecución y control relacionados con el medio ambiente, la ordenación del territorio, los sistemas de transporte y la accesibilidad, los servicios urbanos y la divulgación del patrimonio.