Modelos hidráulicos en el análisis de riesgos de inundación
En España las inundaciones son los desastres naturales con mayor impacto sobre la vida y los bienes, según el Instituto Geológico y Minero de España (IGME). Inundaciones catastróficas como la de Yebra y Almoguera, en Guadalajara (en agosto de 1995); la del camping de Biescas, en el Pirineo de Huesca (en agosto de 1996); o la de Badajoz (en noviembre de 1997) forman ya parte del trágico imaginario colectivo de este país. Y es que el 96% de las víctimas producidas por inundaciones en la segunda mitad del siglo XX derivan de inundaciones torrenciales en pequeñas cuencas (Ayala-Carcedo, 1999). De ahí la necesidad ineludible de las administraciones públicas de generar cartografía de peligrosidad por riesgos de inundación.

El rio Saja con su caudal desbordado ocupando la llanura de inundación en su desembocadura entre las localidades de Miengo y Suances, en Cantabria, España. Imagen: L’irlandés
Para crear estos mapas de zonas inundables es necesario modelizar el comportamiento de los cursos fluviales mediante modelos matemáticos hidrodinámicos apoyados en técnicas GIS. Dentro de los modelos de simulación hidráulica los más conocidos o los que con mayor frecuencia se aplican, son los denominados de análisis 1D o unidimensionales.
En este tipo de modelos la información topográfica e hidráulica se introduce mediante secciones transversales ortogonales a lo largo del río o canal, situados en los puntos donde mejor se define la geometría del cauce y sus márgenes. En ellos se calculan los promedios de velocidad y tirante o calado. Lógicamente cuanto mayores sean estos puntos conocidos mejor será la representación de la realidad, especialmente en zonas con cursos de agua fuertemente curvados o meandriformes. Estos modelos son útiles cuando lo significativo es determinar el nivel máximo o cota que alcanzará la lámina de agua para conocer, por ejemplo, la máxima avenida ordinaria o los diferentes periodos de retorno. Son interesantes principalmente en tramos largos de ríos y canales.
Pero como ya podemos intuir, los modelos 1D presentan una serie de limitaciones derivados de esta dimensionalidad: únicamente son capaces de analizar un flujo constante descendente y siempre perpendicular a las secciones trasversales seleccionadas para la modelización. Es decir, no se tiene en cuenta variaciones en la distribución de velocidades tanto horizontal como verticalmente, ya que toda la sección del río es representada por un único valor medio de velocidad. Por lo general esta metodología de discretización de un río a nivel de secciones hace que programas que utilizan este tipo de modelos, como HEC-RAS, se consideren software robustos, rápidos y numéricamente fiables.
Frente a estos modelos unidimensionales, los modelos bidimensionales o 2D sí que tienen en cuenta estas variaciones en el plano horizontal, promediando los valores para la columna vertical del agua. Permiten modelizar dominios de flujo muy diversos, ya que posibilita incorporar al modelo ambientes complejos, como ríos con marcadas variaciones de velocidad o con flujos transversales. Son especialmente útiles para el cálculo de llanuras de inundación y para analizar flujos con características laminares.
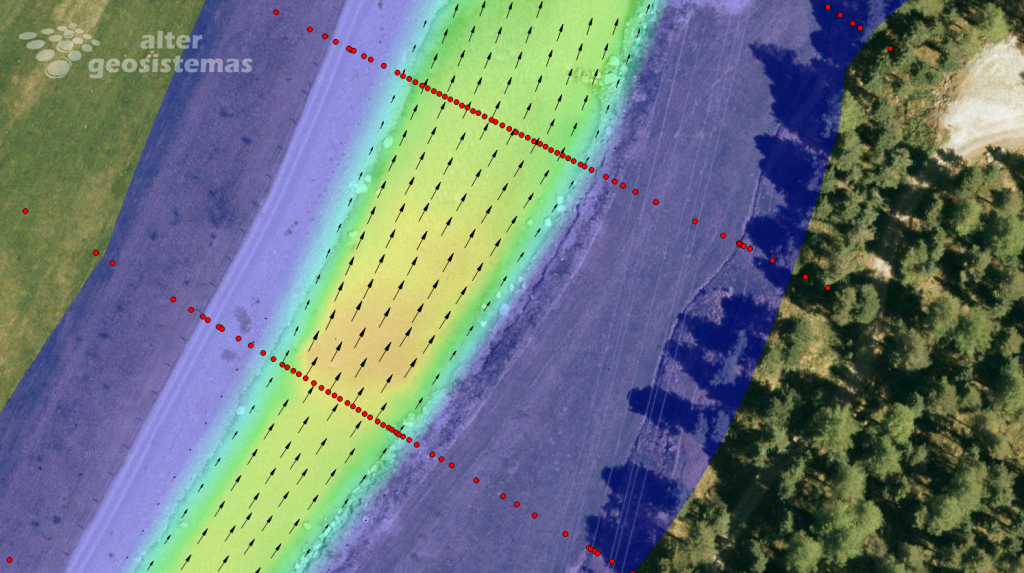
Vectores de dirección, velocidad del flujo de agua en un río y delimitación del área inundable simulado en un modelo bidimensional.
Al ser más complejos que los modelos 1D requieren de un mayor esfuerzo computacional así como de trabajo de preparación, sobre todo a nivel de información espacial: necesitamos una malla derivada de un Modelo Digital del Terreno (MDT) suficientemente precisa (LiDAR, DGPS, fotogrametría, topografía clásica, etc.). Esta información de elevación puede provenir de modelos ráster, los cuales a su vez pueden ser:
- Estructurados, con mallas regulares de los que habitualmente se manejan en los SIG, simples y eficientes, pero torpes para la representación de datos topográficos arbitrarios.
- No estructurados, como mallas compuestas de facetas triangulares, más complejas pero mucho más flexibles para la generación automática de geometrías complejas.

Como se aprecia en la captura de pantalla, los modelos hidráulicos 2D se generan a partir de mallas TIN de facetas triangulares que definen los límites del modelo y en las cuales se integran zonas de diferentes restricciones, líneas de rupturas y áreas no computables
Esta malla deberá de ser más densa y precisa en aquellas zonas donde se producen fuertes cambios en el flujo de la corriente, y menos concisa en aquellas otras de menor interés. Asimismo, deberemos evitar celdas en la malla con fuertes deformaciones.
Las pérdidas de carga continuas por efecto de la fricción se modelizan mediante fórmulas matemáticas. La más conocida es la de Manning, que determina de manera empírica la disminución en velocidad del agua provocado por el rozamiento con el terreno. Su coeficiente se establece a partir de valores recogidos en tablas que indican la rugosidad del tipo de material presente en el cauce y sus márgenes, la vegetación existente, etc.
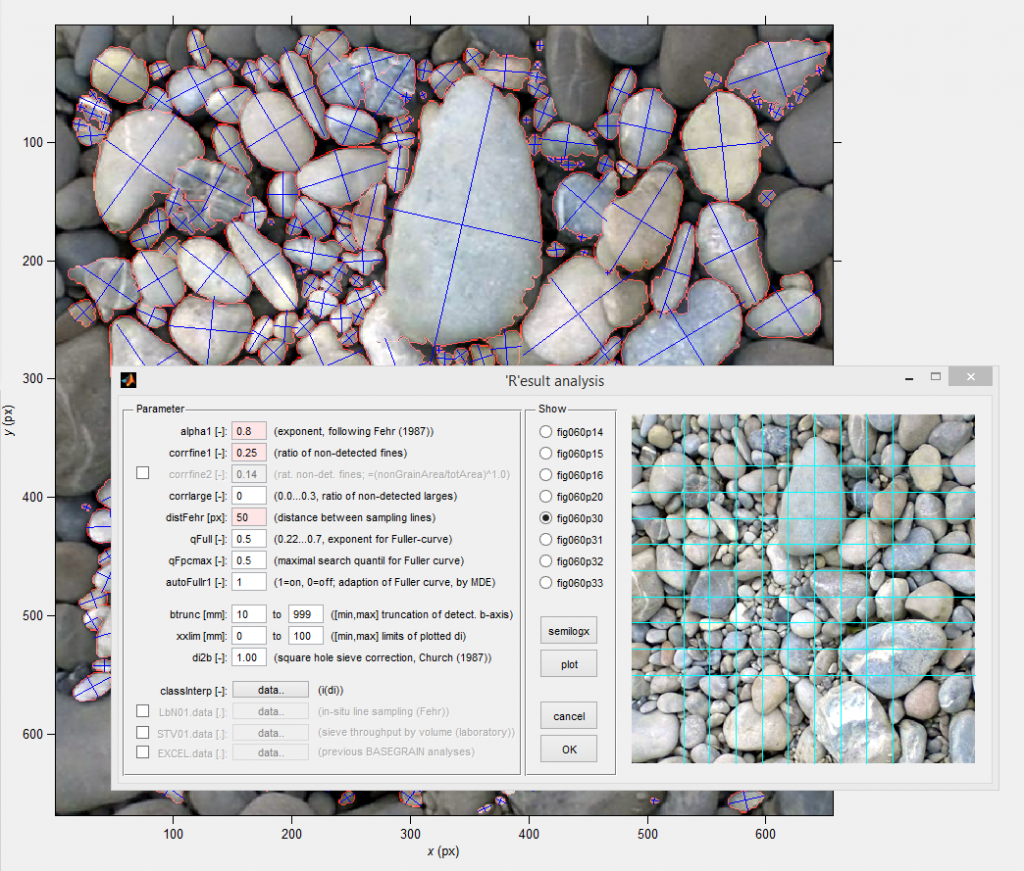
La granulometría del material del lecho de grava fluvial también la podemos determinar a partir programas de análisis de imágenes para tal fin.
Como vemos, frente a los modelos 2D la gran desventaja de los modelos 1D es que cada vez que realizamos un corte transversal del cauce estamos indicando que en este lugar la superficie del agua es igual en toda la sección. El problema viene cuando nos enfrentamos a una condición hidráulica más compleja, con líneas de flujo mucho más difíciles de determinar que pueden inducir a errores en la modelización.
Existe un tercer tipo de modelos denominado tridimensional o 3D, que no he tratado aquí por ser menos utilizados. Son bastante más complejos que los anteriores, al poder calcular la velocidad en sus tres componentes espaciales. Debido al fuerte incremento computacional que esto supone se aplican en zonas donde se requiere de análisis mucho más detallados y no suele ser común usarlos para grandes dominios.

GIS Project Manager en Alter Geosistemas. Es geógrafo con amplia experiencia profesional en el ámbito de la geomática y las tecnologías afines. Ha dirigido y participado en numerosos proyectos de consultoría e ingeniería en las fases de planificación, ejecución y control relacionados con el medio ambiente, la ordenación del territorio, los sistemas de transporte y la accesibilidad, los servicios urbanos y la divulgación del patrimonio.



